Localización

Terminología

La probabilidad de que un evento x ocurra es P(x).

Debe tener un valor entre 0 y 1. 0 <= P(x) <= 1.

Eventos independientes

La probabilidad del primer evento no afecta al siguiente.

Ej.: Girar un moneda.

Eventos dependientes

La probabilidad del primer evento sí afecta al siguiente.

Ej.: Si tú sueles salir afuera cuando hace sol, la probabilidad de que salgas afuera por la noche.

Articulación de probabilidades

La probabilidad de que dos o más eventos independientes ocurran juntos.

Cuantificación de certidumbre o incertidumbre

Por ejemplo, la probabilidad de que un robot de una cierta localización se mueva para una dirección u otra.

Prior probability o probabilidad anterior

La distribución probabilística (explicada más adelante) de por ejemplo la localización de un coche, antes de que se tomen las medidas con los sensores y la probabilidad cambie. Es decir, sin tener en cuenta las evidencias.

Posterior probability o probabilidad posterior

La distribución probabilística después de tener en cuenta ciertas evidencias.

Bayes’ Rule

Dada una predicción inicial, si recolectamos datos adicionales que dependan dee esa predicción inicial entonces podremos mejorar la predicción.

Ejemplo:

Medidas como la velocidad, la dirección y la localización de un coche no las podemos medir perfectamente. Pero algunas se relacionan entre sí. Si queremos saber la localización del coche, podemos reducir la incertidumbre utilizando sensores para reunir datos sobre lo que rodea al objeto (sensores externos -> cámara, lidar y radar) y su movimiento mediante su velocidad (sensor interno).

Aunque la información de los sensores no es perfecta, cuando se combina mediante la Bayes’ rule pueden formar una representación más exacta de la posición del coche, su movimiento y su entorno.

Probability Distribution

Te permite representar la probabilidad de un evento a través de una ecuación matemática. Por lo que pueden ser visualizadas en un gráfico y se puede trabajar con ellas utilizando álgebra, álgebra lineal y cálculo.

Existen dos tipos de distribuciones probabilísticas:

• Discretas
• Continuas

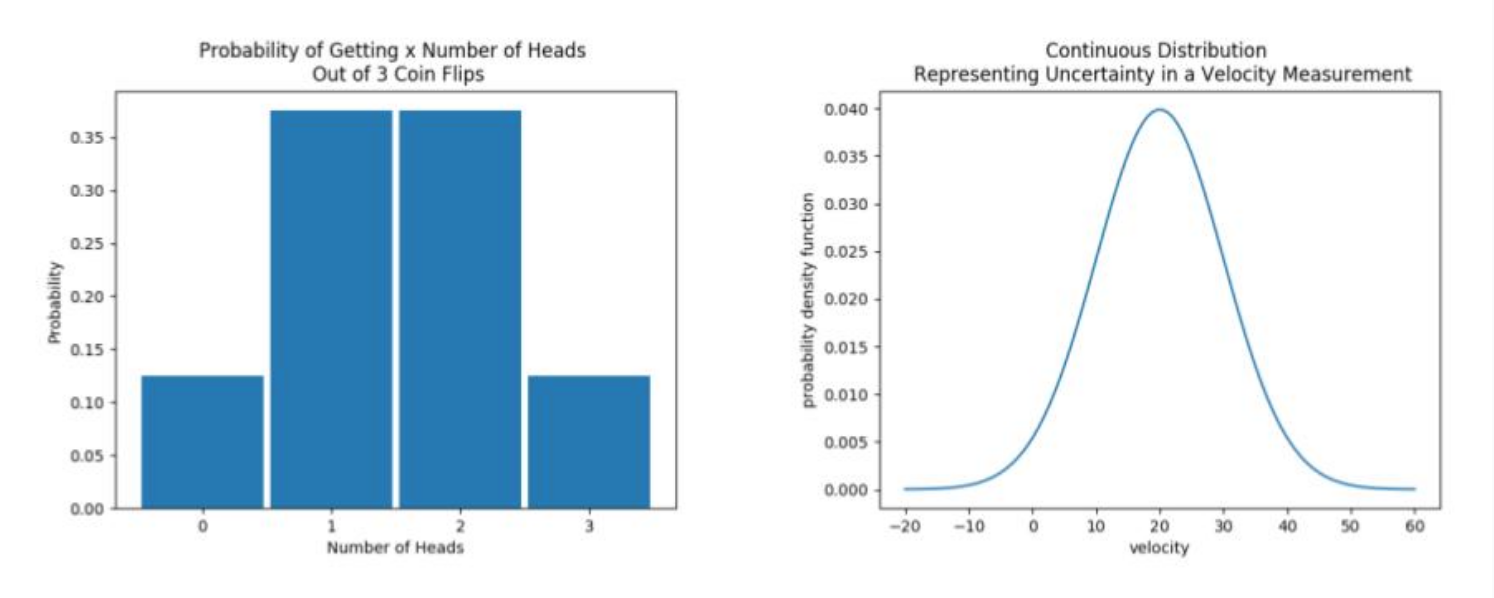
Distribución discreta (izquierda) y distribución continua (derecha) - Imagen de Udacity

Localización

La forma tradicional de resolver dónde se encuentra un coche es mediante señales de satélites, es decir, por GPS (Global Positioning System). Sin embargo, esta forma no es muy precisa con 2 a 10 metros de error, cuando lo que buscamos es que tenga entre 2 a 10 cm de error como máximo.

Para entender cómo hacerlo primero debemos entender la localización:

localization-example-step1.png

1.Distribución probabilística uniforme - Imagen de Udacity

1.En este caso nuestro robot no sabe dónde se encuentra ya que no ha observado su entorno por lo que la probabilidad de que haya una puerta (rectángulo verde) se mantiene constante para todo el entorno, llevando a la máxima confusión al no saber dónde se encuentra.

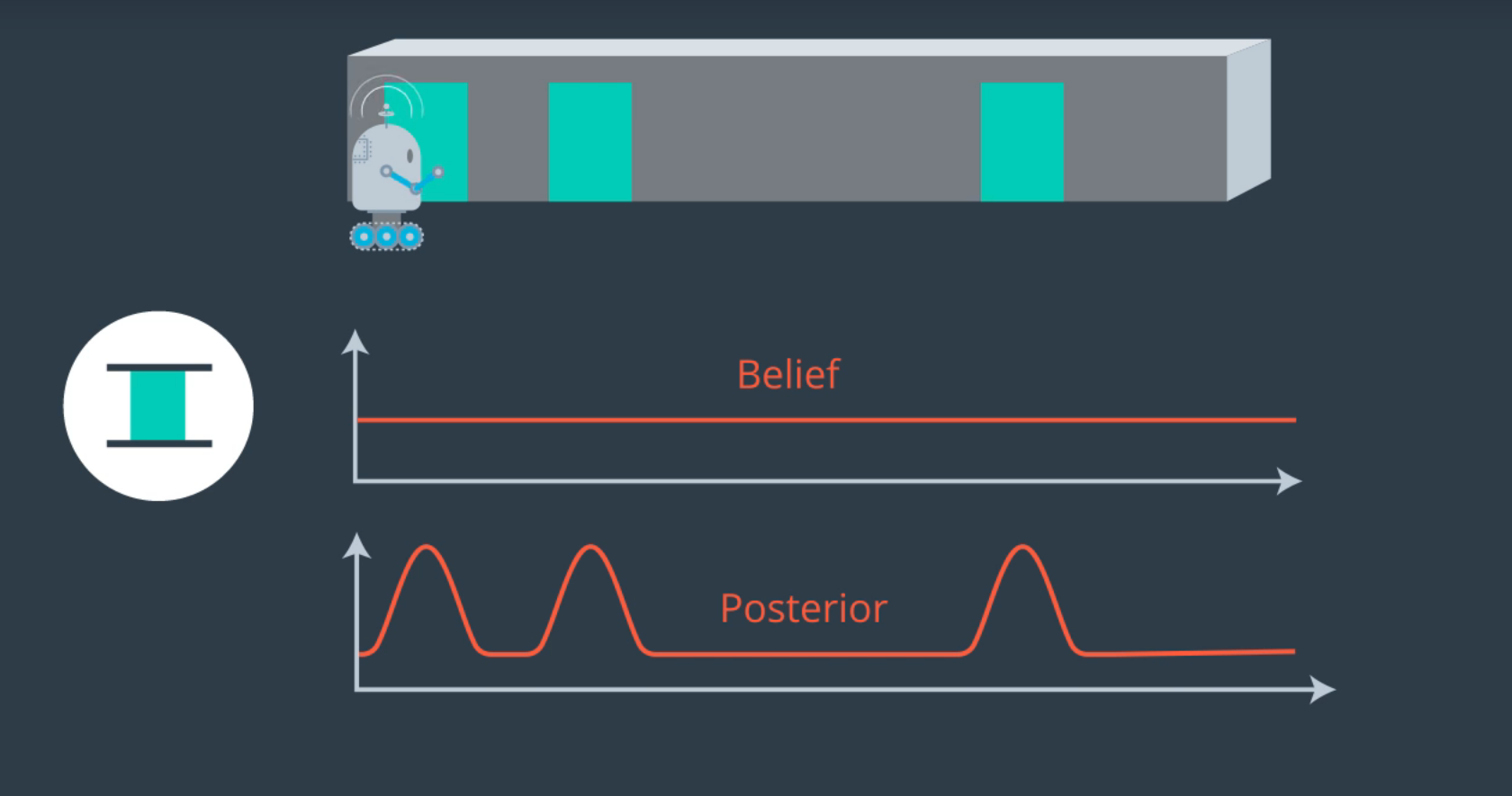
2.Distribución probabilística posterior - Imagen de Udacity

2.El robot ha utilizado sus sensores (por ejemplo la cámara) para “observar” su entorno. De esta forma pudo crear una distribución probabilística para destacar dónde se encuentran las puertas. Aunque todavía puede no saber dónde está y ver una puerta donde no la hay.

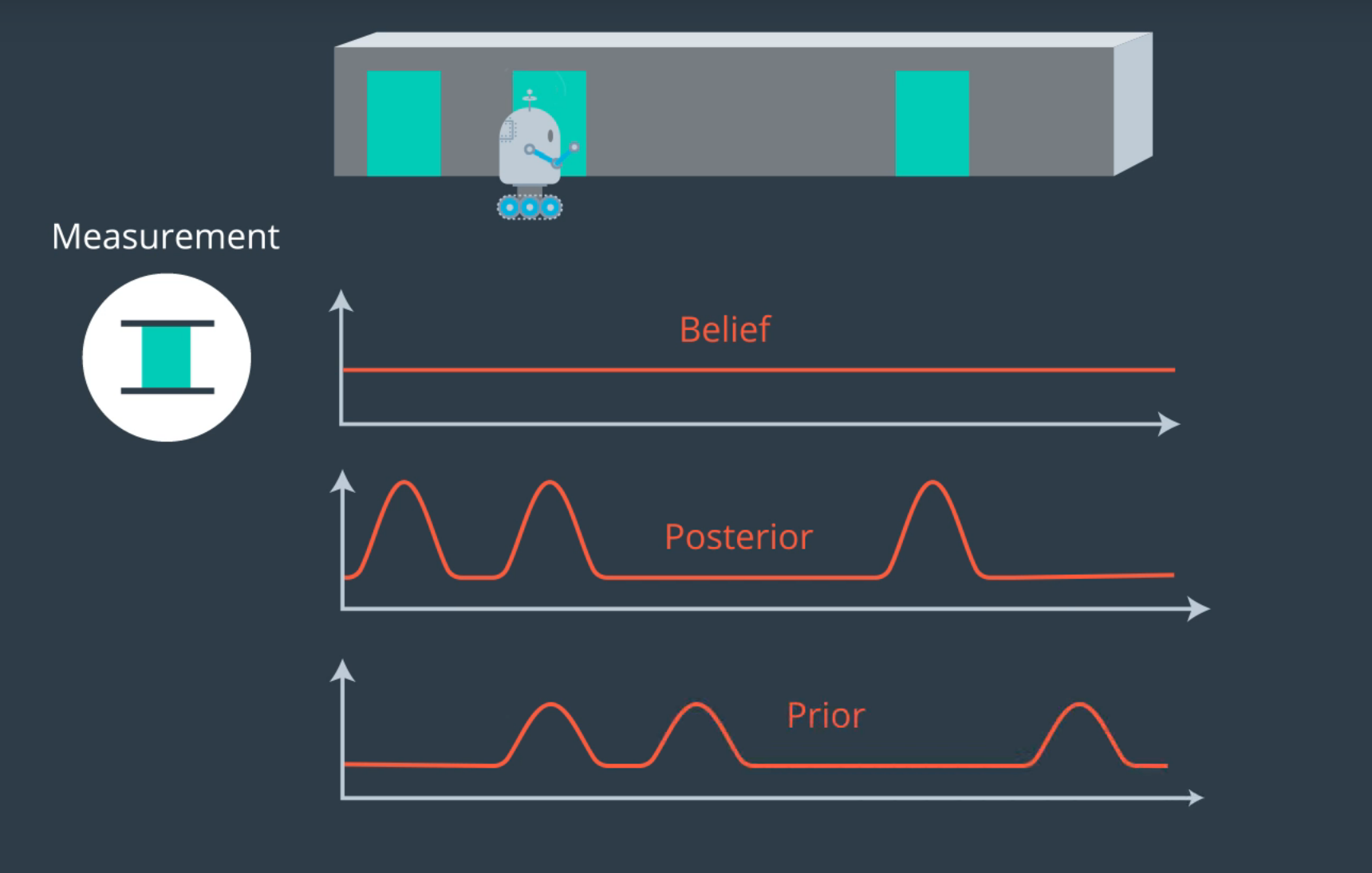
3.Distribución probabilística anterior después de que el robot se mueva hacia la derecha - Imagen de Udacity

3.El proceso de mover los “beliefs” (es decir, dónde se cree que está la puerta) hacia la derecha es llamado convolución. Ahora, al no haber utilizado los sensores para saber dónde se encuentra el robot, ésta se convierte en nuestra distribución probabilística anterior.

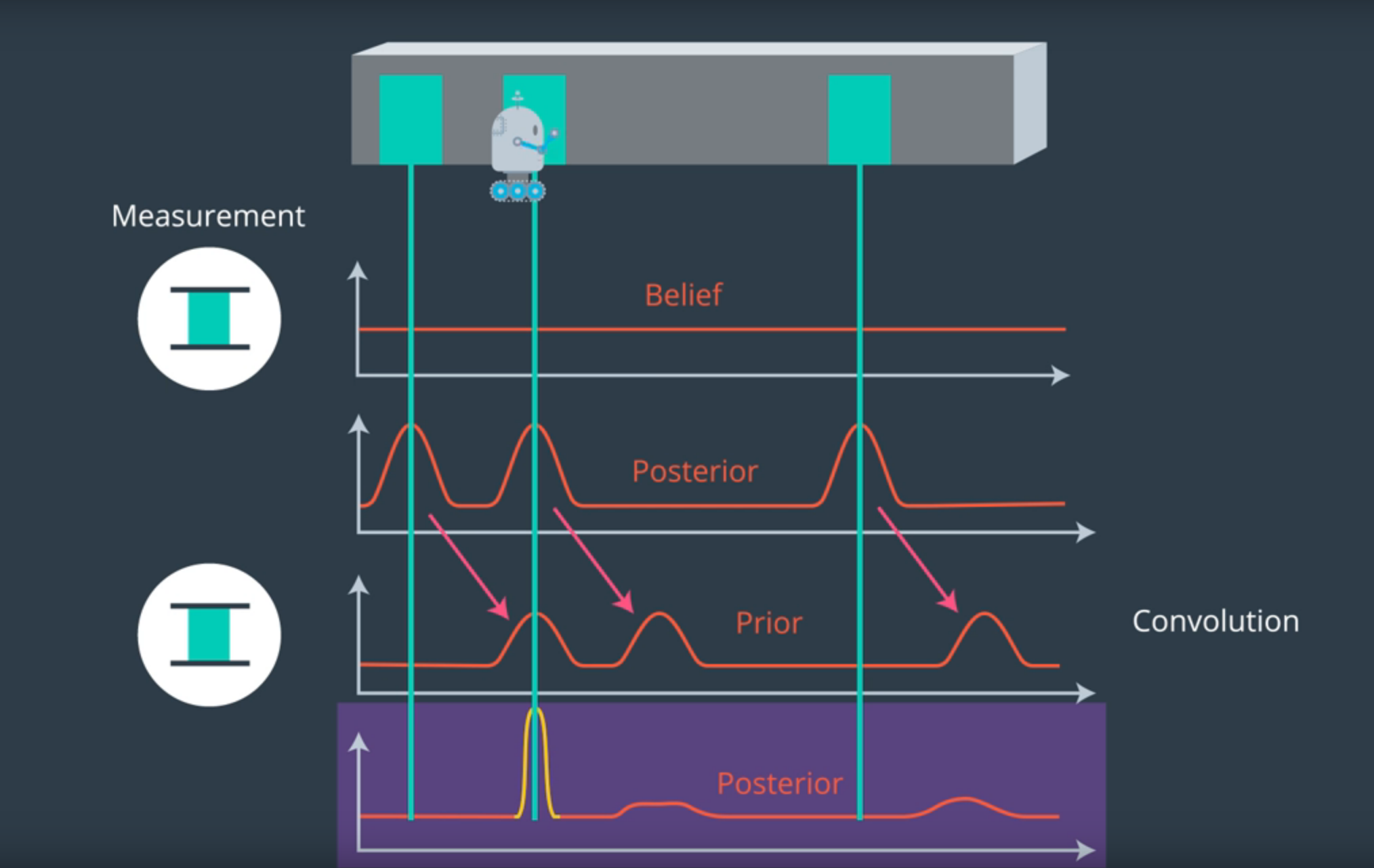
4.Distribución probabilística posterior final - Imagen de Udacity

4.Se multiplica la última distribución probabilística por una función muy parecida a la segunda distribución (la posterior) y da como resultado esta cuarta que presenta una gran probabilidad en la puerta que está cerca de él.

Por lo tanto, el procedimiento principal de localización es el siguiente:

1. Predicción inicial: El robot utiliza los sensores y realiza una actualización de las medidas (Measurement Update) mediante la Bayes’ rule. Se utiliza la normalización para que la distribución probabilística tenga una suma de 1.

2. Measurement Update: Utilizamos los sensores para ver que rodea al objeto, obteniendo información sobre los alrededor y redefiniendo nuestra predicción de la localización.

3. Prediction (or Time Update): Cuando se mueve, realiza una actualización del movimiento prediciendo donde se moverá el coche en base al conocimiento que tenemos sobre su velocidad y posición actual.

4. Repetición.

   

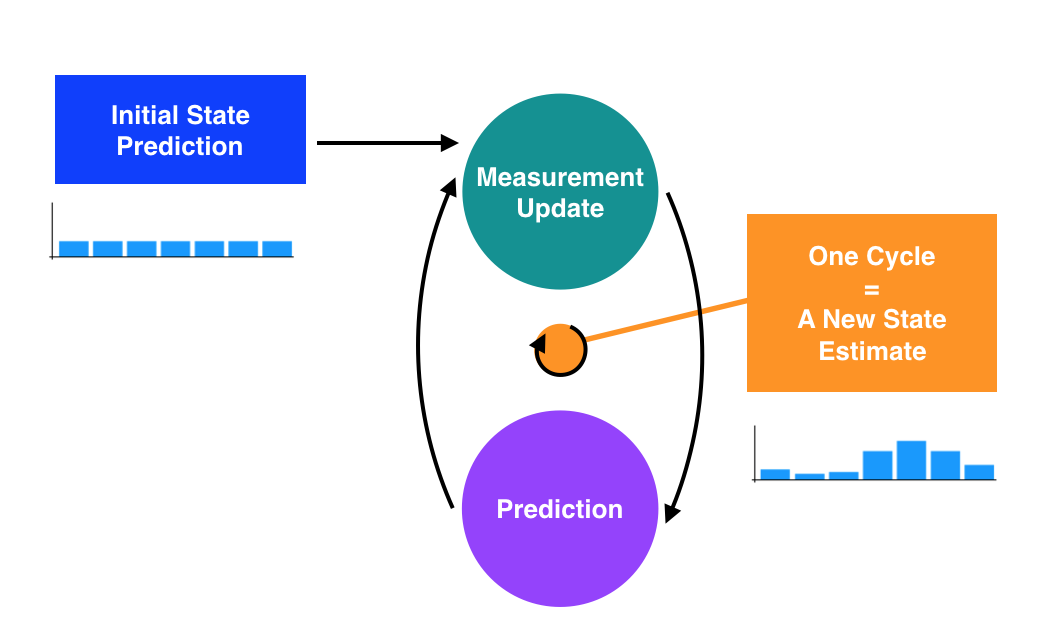
   Pasos de la localización- Imagen de Udacity

Ejercicios de localización en GitHub: GitHub

Ahora pongamos el caso de que tenemos un robot en un espacio unidimensional formado por 5 cuadrados a los que llamaremos desde x1 a x5. Nuestro espacio lo representamos de la siguiente forma: [0,0,1,0,0] donde uno es donde se encuentra nuestro objeto.

El objeto se mueve y dos de las probabilidades son las siguientes:

\[p(x_{i+2} | x_i) = 0.4\]

Probabilidad dos pasos hacia la derecha

\[p(x_{i+1} | x_i) = 0.15\]

Probabilidad un paso hacia la derecha. Y así para el resto de pasos.

Nos daría lugar a un array con los siguientes valores: [0.15, 15, 0.15, 0.15, 0.4], teniendo una mayor probabilidad de que esté en el último cuadrado.

Sin embargo, si se mueve mil pasos, la probabilidad acabaría teniendo a 0.2 en cada elemento haciendo que el elemento no pudiese ubicarse.

A esto lo denominamos entropía y posee la siguiente fórmula:

\[-\sum{p(x_i)*log(p(x_i))}\]