Escrito por Aarón Espasandín

1 minuto de lectura

Matrices y transformaciones del estado

Distribución gaussiana multivariable o de grandes dimensiones:

• La media (mu) es ahora un vector de dimensión D.
• La varianza es reemplazada por la llamada covarianza y es una matriz de D filas y D columnas.

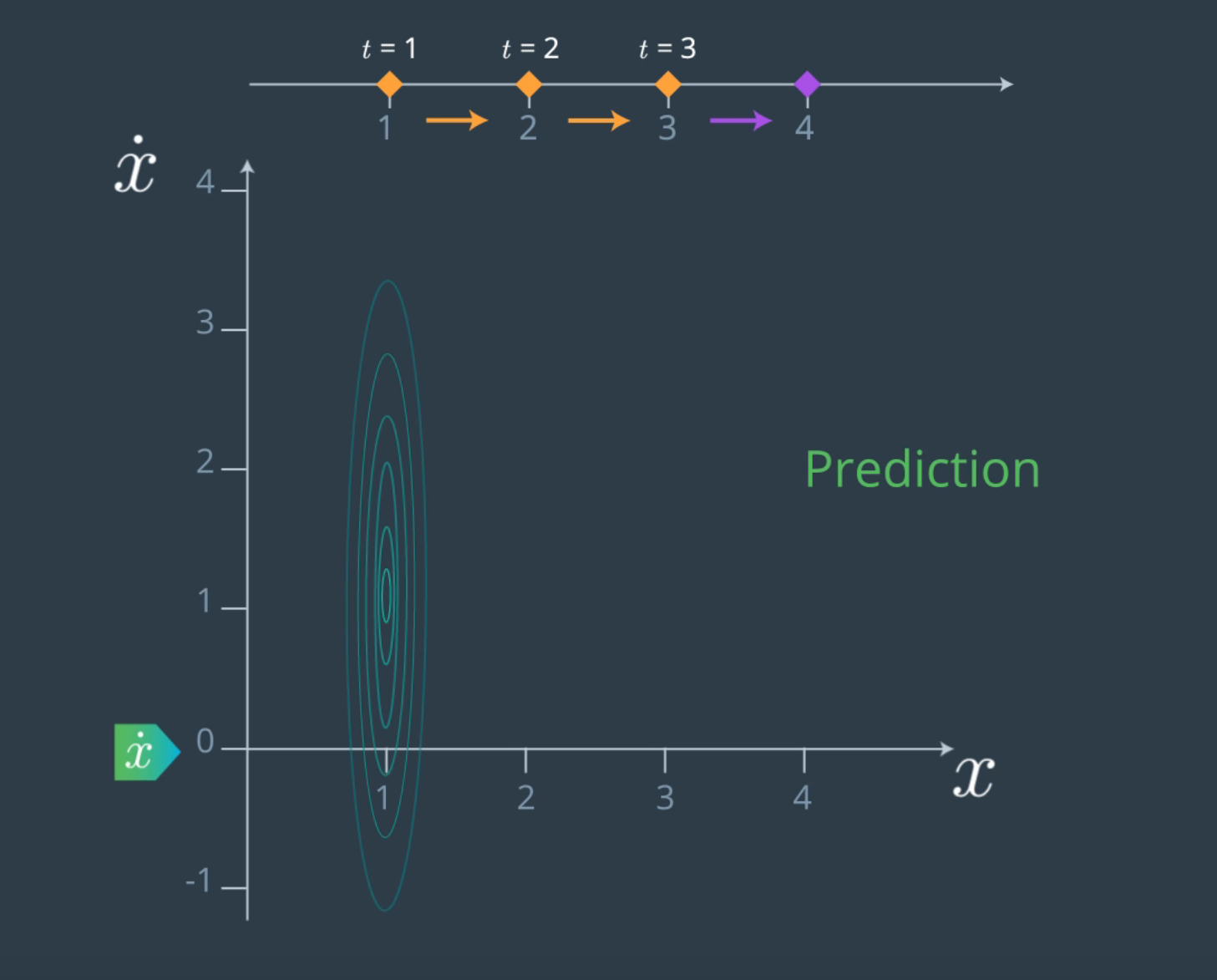
x: posición | x con punto: velocidad
Distribución Gaussiana Multivariable en 2D - Imagen de Udacity

Si a esta distribución le añadimos otra extraída de la información que nos proporcionan los sensores, podríamos de esta forma unir ambas y obtener una nueva más exacta al igual que sucedía en el espacio de una dimensión.

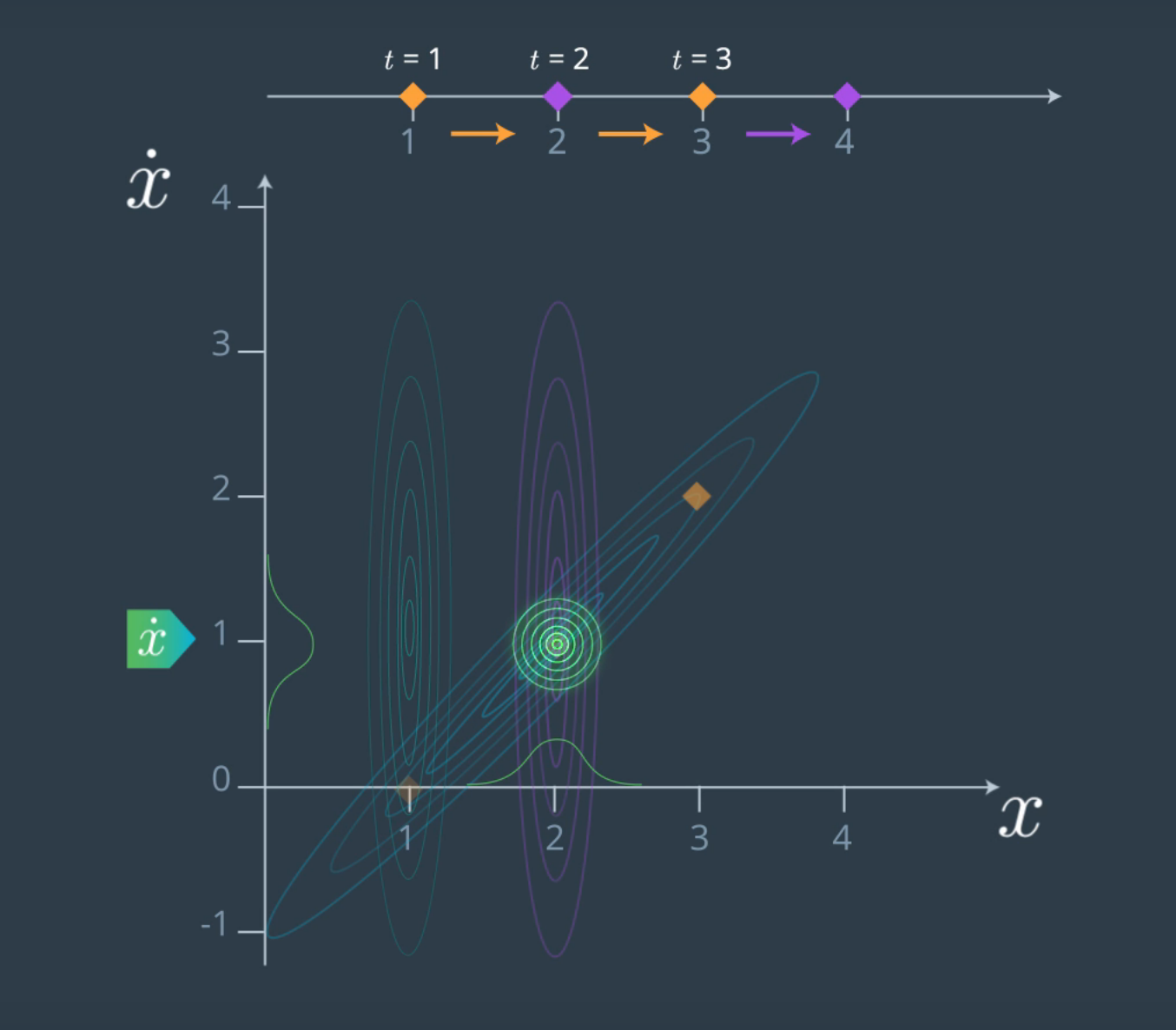
Representación de la distribución gaussiana resultante - Imagen de Udacity

Esta última distribución es el resultado de la multiplicación de la distribución probabilística anterior con la medida.

Si queremos saber entonces la distribución al cambiar de posición deberemos utilizar la siguiente ecuación:

Las variables de los filtros Kalman se suelen denominar estados (states) ya que reflejan los estados del mundo físico como dónde se encuentra un coche y a qué velocidad se está moviendo. Estos estados se separan en dos categorías:

• Observables: Como la localización en un momento preciso.
• Ocultos: Como la velocidad.

Pero gracias a los estados observables podemos obtener información sobre los ocultos.

En futuras seccionas explicaré las matemáticas que se encuentran detrás de la actualización:

Representación matemática de la actualización - Imagen de Udacity