Kalman Filters

Es una técnica para indicar el estado de un sistema, similar a la Monte Carlo localization (utilizada en la anterior sección).

Las diferencias entre ambas son:

• Kalman utiliza una distribución probabilística contínua frente a Monte Carlo que utiliza una discreta.
• Kalman utiliza una distribución uni-modal frente a la multi-modal de Monte Carlo (explico qué son más adelante).

Para inferir la velocidad de un objeto necesitamos ver la posición de un objeto en los frames anteriores para así poder predecirlo.

El filtro Kalman nos da una forma matemática de inferir la velocidad utilizando solamente un set de localizaciones medidas.

Podemos representar la distribución probabilística de este filtro de la siguiente manera:

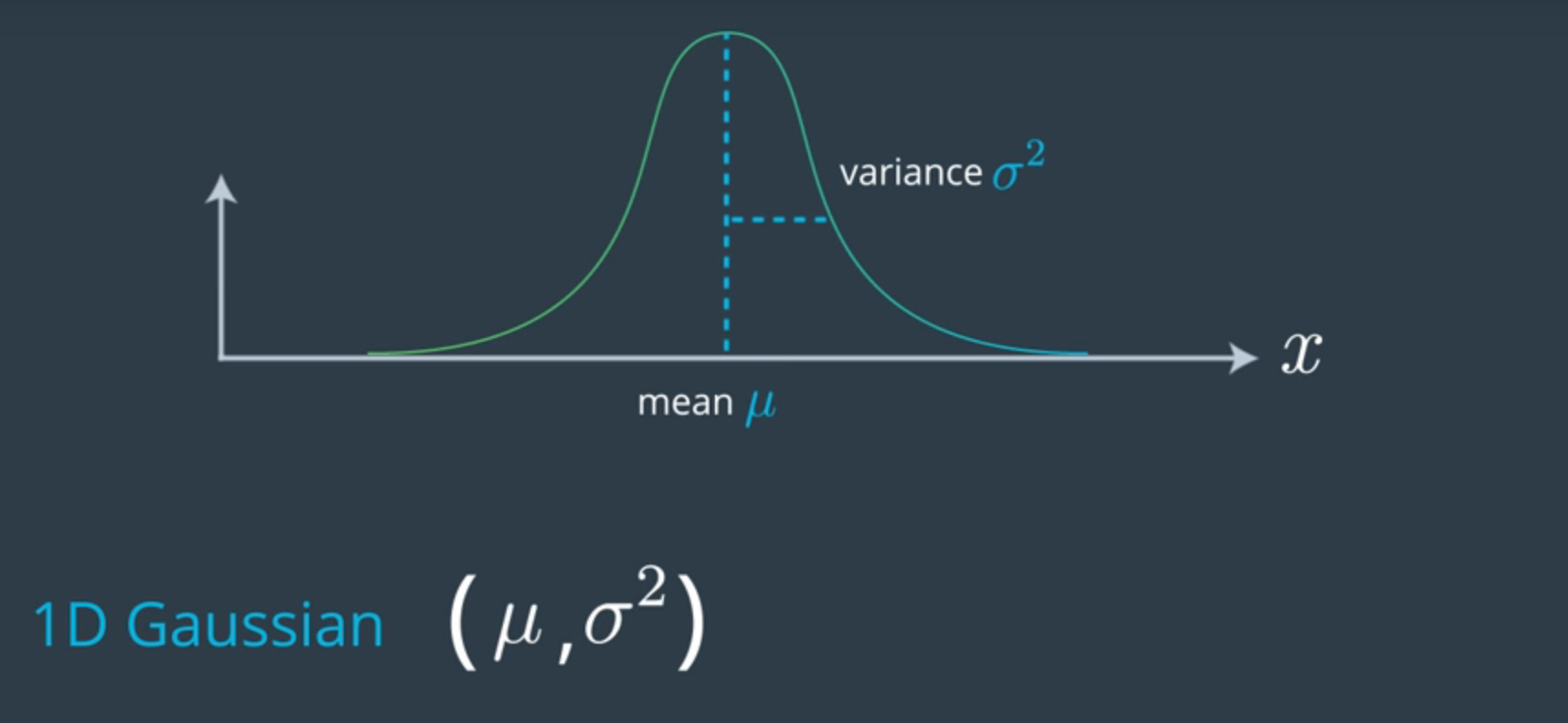
Distribución probabilística contínua del filtro Kalman en 1 dimensión - Imagen de Udacity

Si nos fijamos, el resultado es una distribución gausiana la cual se caracteriza por un único máximo seguido de una caída exponencial en ambos lados de él. Cuanto menor sea la varianza de esta función, menor incertidumbre tendremos.

Siendo la ecuación de la función la siguiente:

\[f(x) = e^{-(x-\mu)²/2\sigma²}\]

Vemos aquí que si x = mu, entonces obtenemos e⁰ que es igual a 1.

Y esta la fórmula de esta función ya normalizada es la siguiente:

\[f(x) = \frac{1}{\sqrt{2\pi\sigma²}}*e^{-(x-\mu)²/2\sigma²}\]

Sobre este filtro también debemos tener en cuenta un hecho que ocurre cuando juntamos dós distribuciones probabilísticas:

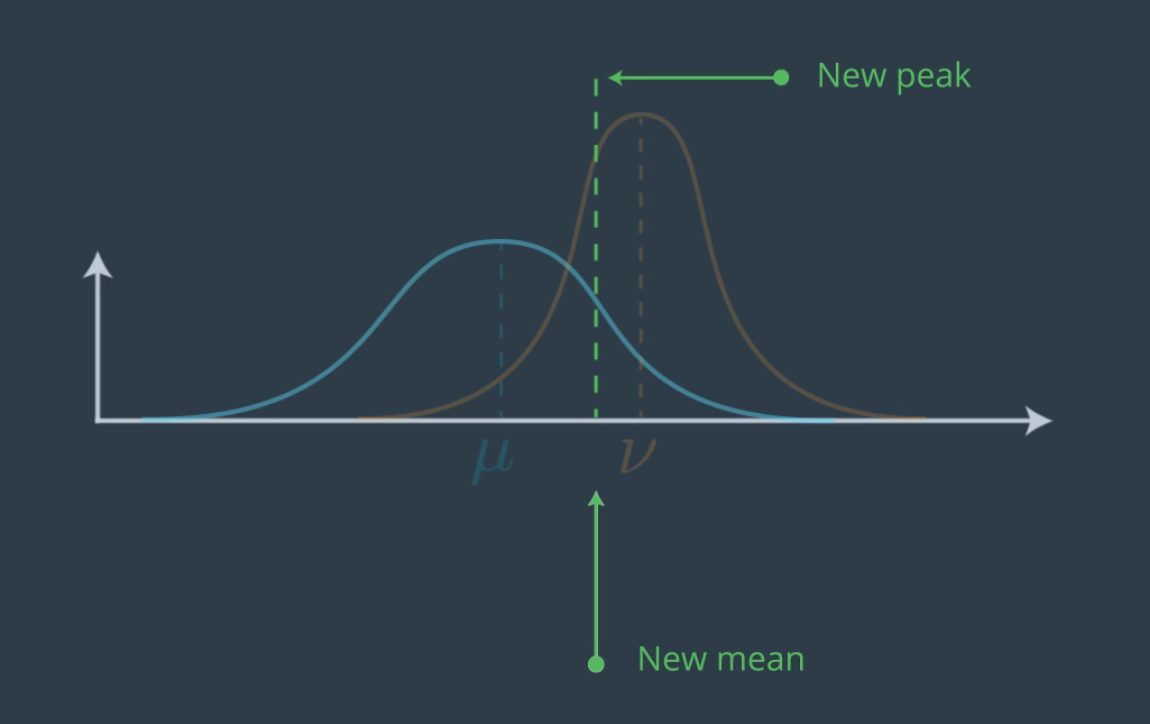
Se junta nuestra medida original (función azul) y una nueva medida obtenida por los sensores (naranja) - Imagen de Udacity

La nueva distribución que da la unión de ambas presenta un mayor “pico” que las anteriores gráficas debido a haber ganado información. Matemáticamente, la varianza y la media de la nueva distribución probabilística se expresa de la siguiente forma:

1ª distribución: mu, sigma².

2ª distribución: nu, r².

3ª distribución: mu’, sigma²’.

\[\mu'= \frac{r²\mu + \sigma²\nu}{r²+\sigma²}\] \[\sigma²' = \frac{1}{\frac{1}{r²}+\frac{1}{\sigma²}}\]

Para calcular una nueva distribución probabilística que se ha desplazado de la inicial, proceso llamado motion update, simplemente debemos sumar sus componentes:

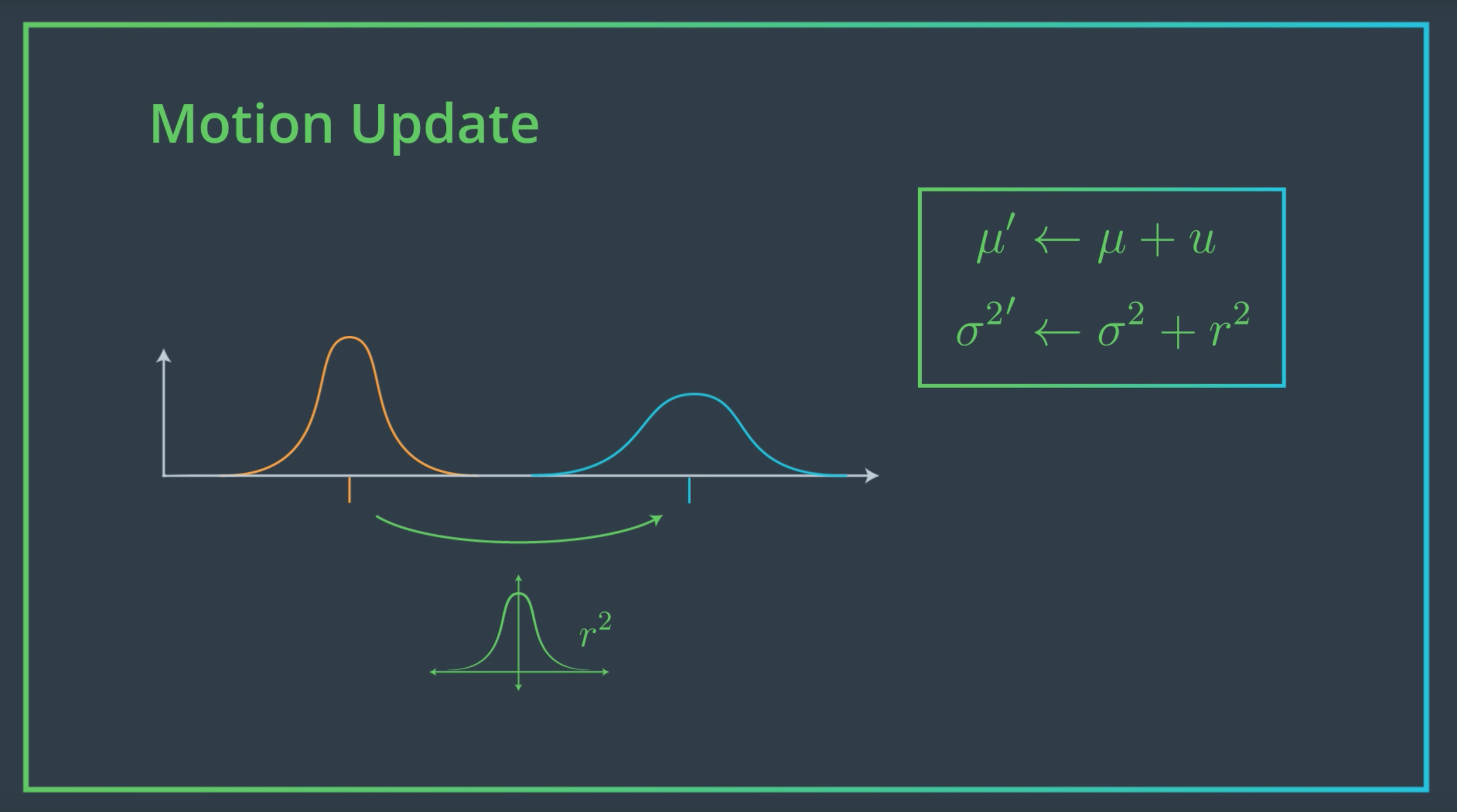
Motion Update - Imagen de Udacity